雖然計算機內部使用二進制來表示各種信息,但計算機與外部的交流仍采用人們熟悉和便于閱讀的形式。接下來我們將討論幾種進位計數制之間的轉換問題。

1 R進制數轉換為十進制數
根據R進制數的按位權展開式,我們可以很方便地將R進制數轉化為10進制數。
【例1】將(110.101)2、(16.24)8、(5E.A7)16轉化為10進制數。
(110.101)2 =1×22 +1×21 +0×20+1×2-1 +0×2-2 +1×2-3
=6.625
(16.24)8 =1×81 +6×80 +2×8-1 +4×8-2
=14.3125
(5E.A7)16 =5×161 +14×160 +10×16-1 +7×16-2
=94.6523
2 十進制數轉化為R進制數
將十進制數轉化為R進制數,只要對其整數部分,采用除以R取余法,而對其小數部分,則采用乘以R取整法即可。
【例2】將(179.48)10化為二進制數。
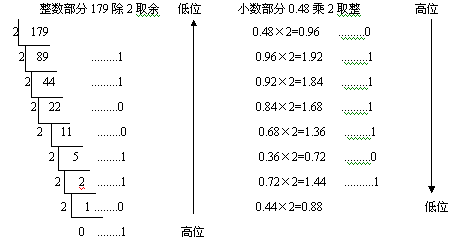
其中,(179)10=(10110011)2(0.48)10=(0.0111101)2(近似取7位)
因此,(179.48)10=(10110011.0111101)2
從此例我們可以看出,一個十進制的整數可以精確轉化為一個二進制整數,但是一個十進制的小數并不一定能夠精確地轉化為一個二進制小數。
【例3】將(179.48)10化為八進制數。

其中,(179)10=(263)8 ,(0.48)10=(0.365)8(近似取3位)
因此,(179.48)10=(263.365)8
【例4】將(179.48)10化為十六進制數。
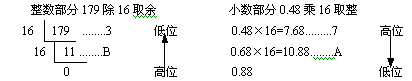
其中,(179)10=(B3)16,(0.48)10=(0.7A)16(近似取2位)
所以,(179.48)10=(B3.7A)16
與十進制數轉化為二進制數類似,當我們將十進制小數轉換為八進制或十六進制小數的時候,同樣會遇到不能精確轉化的問題。
3 二進制、八進制、十六進制數之間的轉換
因為8=23,所以需要3位二進制數表示1位八進制數;而16=24,所以需要4位二進制數表示1位十六進制數。由此我們可以看出,二進制、八進制、十六進制之間的轉換是比較容易的。
1)二進制和八進制數之間的轉換
二進制數轉換成八進制數時,以小數點為中心向左右兩邊延伸,每三位一組,小數點前不足三位時,前面添0補足三位;小數后不足三位時,后面添0補足三位。然后將各組二進制數轉換成八進制數。
【例5】將(10110011.011110101)2化為八進制。
(10110011.011110101)2 = 010 110 011.011110 101= (263.365)8
八進制轉換成二進制數則可概括為“一位拆三位”,即把一位八進制寫成對應的三位二進制,然后按順序連接起來即可。
【例6】將(1234)8化為二進制數。
(1234)8=1 2 3 4=001 010 011100=(1010011100)2

2) 二進制和十六進制數之間的轉換
類似于二進制轉換成八進制,二進制轉換成十六進制時也是以小數點為中心向左右兩邊延伸,每四位一組,小數點前不足四位時,前面添0補足四位;小數點后不足四位時,后面添0補足四位。然后,將各組的四位二進制數轉換成十六進制數。
【例7】將(10110101011.011101)2轉換成十六進制數。
(10110101011.011101)2=0101 10101011.0111 0100 =(5AB.74)16
十六進制數轉換成二進制數時,將十六進制數中的每一位拆成四位二進制數,然后按順序連接起來。
【例8】將(3CD)16轉換成二進制數。
(3CD)16=3 C D=0011 11001101=(1111001101)2
關于八進制與十六進制之間的轉換,通常先轉換為二進制數作為過渡,再用上面所講的方法進行轉換。
【例9】將(3CD)16轉換成八進制數。
(3CD)16=3 C D=0011 11001101=(1111001101)2 =001 111 001 101=(1715)8